Numeri e fattori primi

Cosa sono i numeri primi?

In un precedente articolo abbiamo già introdotto i numeri primi. I numeri Interi o Naturali sembrano entità scontate, banali quasi, ma in realtà non è così,. Cominciamo col definire che in matematica, un numero primo è un numero intero maggiore di 1 che sia divisibile solamente per 1 e per sé stesso; al contrario, un numero maggiore di 1 che abbia più di due divisori è detto composto. Vediamo di ragionarci un po’ sopra. Prendiamo un numero qualunque ad esempio il 18. Possiamo esprimere questo numero come prodotto di altri numeri.

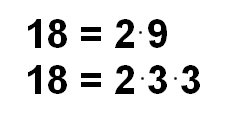
I numeri 2, 9, 3 sono divisori o fattori. Così diremo anche, ad esempio, che il 3 è un divisore di 12. Perché dividendo 12 per 3 otteniamo un numero intero 4 e che il resto della divisione è zero. Ritornando all’esempio del 18 diremo che il 2 o il 3 si chiama anche “fattore” perché permette di costruire il numero 18. I divisori di 18 sono 1, 2, 3, 6, 9, 18. Infatti, 18 diviso per ognuno di essi dà un numero intero, e fra tutti i divisori dobbiamo considerare anche 1, visto che tutti i numeri sono divisibili per 1 e per sé stessi. Se vogliamo trovare i possibili divisori del numero 13, gli unici che troveremo sono l’1 e lo stesso 13. Stessa cosa succede per numeri come 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 …. e così via, tutti questi sono i numeri primi e ce ne sono infiniti. Riferendoci all’articolo precedente, possiamo dire alfine che esistono dei numeri speciali che abbiamo definito con nome e proprietà, compiendo appunto un’operazione di astrazione. Lo studio che ancora oggi si compie su questi numeri è molto grande.

I mattoni della matematica.

I numeri primi vengono a volte definiti “i mattoni della matematica”, poiché sono elementi primigeni da cui si genera qualcosa, cioè altri numeri. Ma come siamo arrivati a ciò? Un numero dunque può scomporsi in fattori, così 18 = 2 x 9. Quando utilizziamo il termine “fattore” stiamo pensando al fatto che con 2 e 9 possiamo formare il 18 e lo potremmo costruire anche con altri numeri.

18= 2 x 9 = 3 x 6 = 2 x 3 x 3

Questo processo viene chiamato “scomposizione del numero nel prodotto dei suoi fattori”. In base a questo gli unici fattori di un numero primo sono 1 e il numero stesso. Quando un numero si ripete scriviamo la sua potenza: 3² = tre elevato alla seconda 2⁵= due elevato alla quinta e così via. Ora è chiaro che riguardo al 10 solo la scomposizione 2 x 3 x 3, contiene solo fattori primi.

Ora dato un numero qualunque si può trovare sempre una scomposizione in fattori primi? La risposta è si! Nel caso in cui abbiamo un numero primo ciò è evidente. Ma anche nel caso di tutti gli altri numeri abbiamo il “Teorema Fondamentale dell’aritmetica” dovuto ad Euclide “Ogni numero naturale si può scomporre in un unico modo come prodotto di fattori primi”.

Dimostrazione dell’esistenza

Come abbiamo visto dalla definizione di numero primo si deduce che ogni numero ≥ 2 o è un numero primo o si può esprimere come prodotto di numeri primi. Ciò si può dimostrare per induzione:

• n=2 è primo, quindi soddisfa quanto enunciato.
• Supponendo vero l’enunciato per tutti i numeri da 2 a n, dimostriamo che vale anche per n+1. Per n+1 ci sono due possibilità: o è primo oppure è divisibile per un numero a compreso tra 2 e n. Nel caso in cui n+1 sia divisibile per a per l’ipotesi induttiva o a è primo oppure a ha un divisore primo p. In quest’ultimo caso (per la proprietà transitiva della divisibilità) p è anche un divisore di n+1. In ogni caso, dunque, o n+1 è primo o è divisibile per un primo.

La dimostrazione dell’esistenza della fattorizzazione per ogni numero procede ancora per induzione:

• n=2 è primo e dunque è già banalmente fattorizzato.
• Supponiamo vera l’esistenza di una fattorizzazione per tutti i naturali compresi tra 2 e n e dimostriamola vera anche per n+1. Considerando n+1, abbiamo due casi: n+1 è primo (e quindi è già fattorizzato) oppure n+1 è divisibile per un primo p (come dimostrato nella prima parte); in quest’ultimo caso il numero m=(n+1)/p è minore di n+1, e quindi verifica l’ipotesi induttiva, ovvero esiste una fattorizzazione di m. Ma allora n+1=mp cioè n+1 è fattorizzabile (è il prodotto di m e p).

Quindi l’esistenza di una fattorizzazione è dimostrata per ogni numero naturale n.

La dimostrazione dell’unicità la tralasceremo, chi vuole approfondire la può trovare ovunque, anche su wikipedia.

Scomposizione in fattori primi

Il metodo che si segue per fare una scomposizione in fattori primi consiste nel mettere il numero a sinistra di una linea verticale. Quindi si prova per vedere se il numero è divisibile per 2, 3, 5 … cioè per numeri primi, iniziando dal più piccolo. Nel caso in cui sia divisibile si pone il risultato della divisione sotto il numero dato sempre alla sinistra della linea e il numero per cui si è diviso alla destra della linea e si inizia di nuovo con questo procedimento. Si prosegue fin quando il numero di sinistra è l’unità. Nella colonna di destra appaiono i numeri primi che riducono in fattori il numero dato.

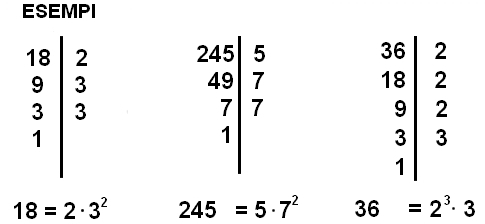
Così quando si scrive 36 = 2³ x 3, affermiamo che è l’unico modo possibile di fare la scomposizione con fattori primi. Quindi il Teorema fondamentale è giustificato ed è uno dei pilastri su cui si fonda l’aritmetica. La parola “primo” viene dal latino primus e intende il concetto di “primario”, “primitivo”, originario, poiché tutti i numeri si possono ottenere a partire da essi. Un qualche tipo regola che permette di raggrupparli senza fraintendimenti , non esiste. Appaiono sempre come un insieme senza apparente ordine e si distribuiscono in maniera casuale nei numeri naturali.